5 (عدد)

• 5 هو ثالث عدد أولي. بما أن 2²¹ + 1، فإن 5 هو عدد أولي لِفيرما. ذلك يجعل من مضلع منتظم ذي خمسة أضلاع منتظم (مخمس أو نجمة خماسية) قابلا للإنشاء بالمسطرة والبركار. وكذلك، يجعل من زاوية ما، قابلة للقسمة على خمسة أجزاء متساوية.

• 5 هو ثالث عدد أولي لِصوفي جيرمين لأن 5*2+1=11 و11 أولي. وهو أول عدد أولي آمن.
• 5 هو ثالث عدد لِكاتالان.
• 5 هو ثالث قوة لعدد أولي لِميرسين وأول عدد أولي لِويلسون.
• 5 هو ثالث عدد أولي عاملي لأن 5 = 1-!3. وهو عدد عاملي بالتناوب، وعدد أولي جيد.
• 5 هو عدد أولي لِأيزنشتاين. وهو العدد الوحيد الذي ينتمي إلى زوجين أوليين توأمين في نفس الوقت.
• 5 هو وتر مثلث قائم بعداه 4 و3.
• يُعتقد أن 5 هو العدد غير الملموس الفردي الوحيد (ليس مجموع قواسم أي عدد طبيعي). وهو ينتمي إلى متتالية أقليدس مولين. وهو أول عدد أولي لِوولستينهولم.
• 5 هو خامس حد في متتالية فيبوناتشي، لكونه مساويا لمجموع اثنين وثلاثة. وهو الحد الوحيد الذي يساوي رتبته في هذه المتتالية.

• 5 هو عدد تشكيلي لأن 5² = 25. وهو عدد سعيد في نظام العد العشاري والخماسي والثنائي والرباعي والسداسي والسباعي والتساعي. وهو عدد كابريكار في نظام العد الثلاثي و السداسي. و هو عدد التقسيمات الصحيحة للعدد 4.
• في نظام العد الخماسي و العشاري و الخماسي عشر ... كل عدد رقم آحاد مضاعف ل 5 مثل 0 و 5 و a و f... مضاعف لـ5. مثال: 15, 10₅=5 , 75 = 5a_15, بما أن 10=5${\displaystyle \cdot }$2 فإن عدد أرقام الجزأ العشري للعدد ${\displaystyle {\frac {1}{5^{n}}}}$ حيث n عدد صحيح هو n. و أرقامه هي ^1-2ⁿ. مثال: ${\displaystyle {\frac {1}{5^{3}}}={\frac {1}{125}}=0.008;8=2^{3}}$ ^[1]
• 5 هو عدد لِبيل وعدد لِماركوف في نفس الوقت بما أنه حل للمعادلات الدافيوتية (1, 2, 5), (1, 5, 13), (2, 5, 29), (5, 13, 194), (5, 29, 433)...
• 5 هو ثاني عدد لِسيربنسكي من النوع الأول ويكتب على الشكلS2 = (2²) + 1.
• ورابع عدد ذا قوس الظل غير القابل للاختزال (Størmer number) .
• 5 له الكتابة ${\displaystyle (1+2i)(1-2i)=(2+i)(2-i)=5}$. و له كتابة في صيغة مربعين 5=2²+1²
• 5 عدد مضلعي. فهو عدد مخمسي و عدد مربعي ممركز و عدد هرمي رباعي و عدد هرمي مثلث رباعي الأبعاد (pentatope number). يمكن لأي عدد صحيح طبيعي أن يكتب في صيغة مجموع 5 أعداد مخمسية.
• في الجبر، مبرهنة أبيل-روفيني هي مبرهنة رياضية تنص على أنه ليس هناك حلولا جبرية للمعادلات الحدودية انطلاقا من الدرجة الخامسة".
• حسب كوراتوفسكي, يكونالمخطط مستويا إذا لم يتضمن زمرة من الرتبة الخامسة.

هندسة

• عدد المجسمات الأفلاطونية المنتظمة هو 5:

• يوجد مجسمان ذا 5 سطوح : موشور مثلثي و هرم مربع ^[2]

• يوجد مضلعان منتظمان ذا 5 أضلاع. المخمس و النجمة الخماسية. و كلاهما قابلان للبناء بالمسطرة و البركار.

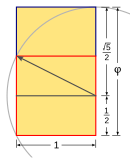
• للرقم 5 علاقة بالنسبة الذهبية (φ) فالنسبة بين ضلع مخمس و البعد بين رأسين غير متتاليين فيه يساوي النسبة الذهبية, كما أن النسبة الذهبية تساوي ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$

الرمز

 

تطور الرمز^[3]

تاريخ تطور الرمز (5) الحديث لا يمكن تعقبه بدقة كبيرة لأنه لم يكن مشابها في البداية للمتتالية المستخدمة في الأرقام من 1 إلى 4 في عهد الهنود. بعد ذلك فيإمبراطورية كوشان و إمبراطورية جوبتا في الهند تعددت رموز العدد 5 و لم تشابه الرمز القديم. في اللغة البنجابيةو اللغة الديوَناكَرية استخدموا بعض الرموز المشابهة للرمز (પ). ثم طوره العرب ليجعلوه مشابها بين (4) و (3). و من خلال جميع تلك الرموز جائوا برمز 5 الحديث.

في العلم

عدد الزوائد عند نجم البحر هو 5

أصابع يد الإنسان خمسة.

 

• 5 هو العدد الذري للبورون
• 5 هو عدد الزوائد عند نجم البحر
• أكبر إعصار صنف من الدرجة الخامسة.
• معظم البرمائيات و الزواحف و الثديات يملكون 5 اصابع في كل يد أو قدم
• أول الكواكب العملاقة الغازية في النظام الشمسي "المشتري" هو الكوكب الخامس حسب بعده عن الشمس
• لمجرة درب التبانة خمسة أذرع أساسية : ذراع حامل رأس الغول و ذراع الدجاجة المجري و ذراع قنطورس و ذراع رامي القوس و ذراع الجبار
• تنصف الفقريات إلى خمس شعب : الثديات و الزواحف و الأسماك و الضفدعيات و الطيور
• 5 هو عدد حواس الإنسان حسب مستوى التعليم الابتدائي. بالرغم من وجود حواس أخرى كالأذن الداخلية.
• توجد 5 نقاط لاغرانج في نظلم ثنائي الأجسام

في الدين

الإسلام

• أركان الإسلام خمسة.
• الصلوات المفروضة خمسة.

ذكر الرقم خمسة في القرآن بلفظ خمسة مرتين في حين ذكر بالصفة الترتيبية الخامسة مرتين أيضاً، ومجموع مرات الذكر أربع مرات، كما ذكر مقلوبه الخُمس (1/5) مرة واحدة.^[4]

ملاحظات